因数分解 中学 応用 119285

中学数学 多項式 の教え方 因数分解の応用問題
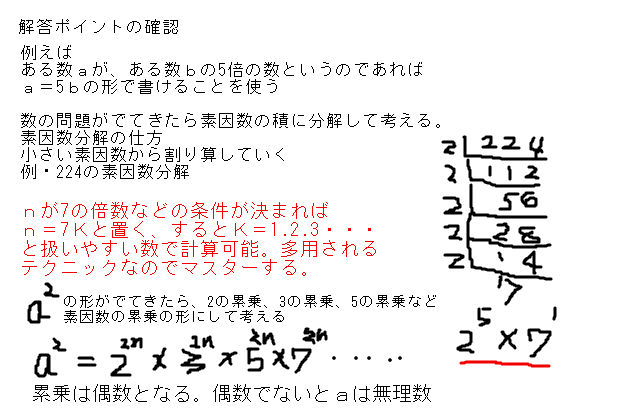
因数分解の問題の解き方とコツ。 2乗・3乗公式とたすきがけ 数の中には「2つ以上の数のかけ算」に変形できるものがたくさんあります。 例えば x 2 − 1 は ( x 1) ( x − 1) というかけ算に変形できますよね。 このように 特定の数を「2つ以上の数のかけ算動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru
因数分解 中学 応用
因数分解 中学 応用- ここで、因数分解の公式①です。 「足して-b-c、掛けて bc 」になる2数を探せばよい ということになりますが、それは「-bと-c 」です。 それで、こうなります。 a2 bc − ab− ac = a2 a(−b− c) bc = (a − b)(a −c) (2) (2) a 2 b c − a b − a c = a 2 a ( − b − c) b c = ( a − b) ( a − c) 式(1)と式(2)で結果が違う? ・・・ よく見ると、式(1)と式(2)で 数学宣教師 ザピエル今回は、こんな質問をいただきました!ハムちゃん\( ab(x y) a(y x) \) を因数分解してください数学宣教師 ザピエル最近は、因数分解関係の問題をよく聞かれ

因数分解 工夫して計算する問題です 分からないので教えてください Clearnote
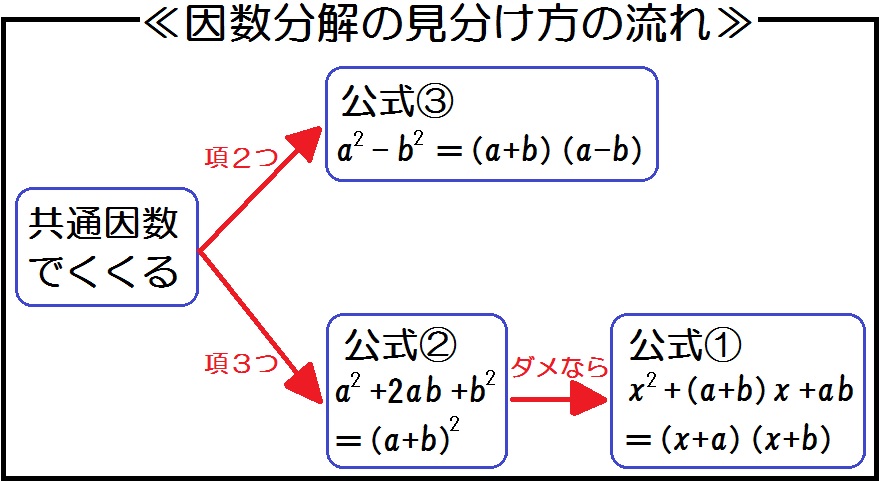
因数分解の応用 2つに分けて共通因数から考える因数分解や、因数分解を2段階行うなどの応用問題について学習します。 ( )でまとめる因数分解 分けて解く因数分解 因数分解の応用 因数分解の応用 因数分解の応用 因数分解の応用 因数分解の応用 相似 (応用問題) 中3数学 相似を利用した発展問題で、実力テストレベルの難易度です。 補助線を引いて面積比を使います。 このレベルの問題が解けるようになったら自信をもって大丈夫ですよ。の形にします. ところで,積が −b 2 bx になるものは何かというと,それは全体の大きな因数分解をしている中で,定数項 −b 2 bx を2つの式の積に分けるということで,それは −b 2 bx をあらかじめ因数分解しておくということです. −b 2 bx=b (x−b) ここで, b (x−b)=x となって和が x になっています. 結局 a 2 x a −b 2 bx = a 2 x a b (x−b) = ( a b) ( a x−b) (答
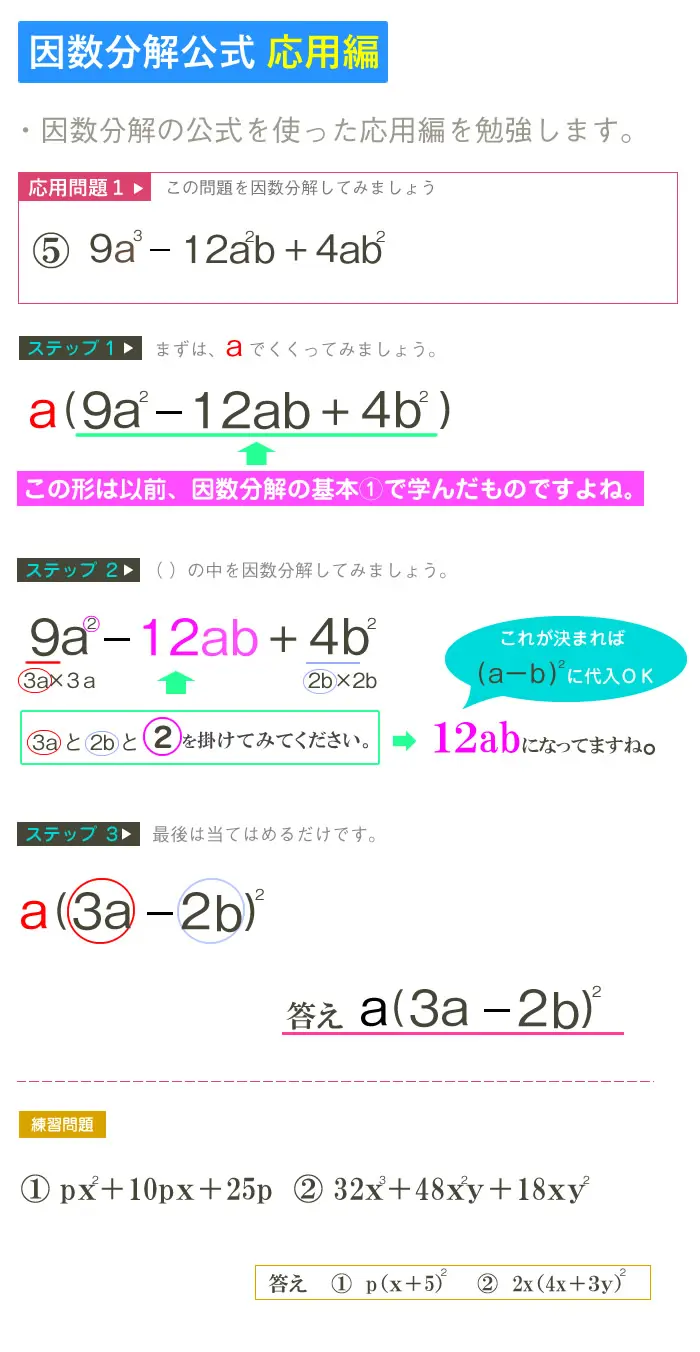
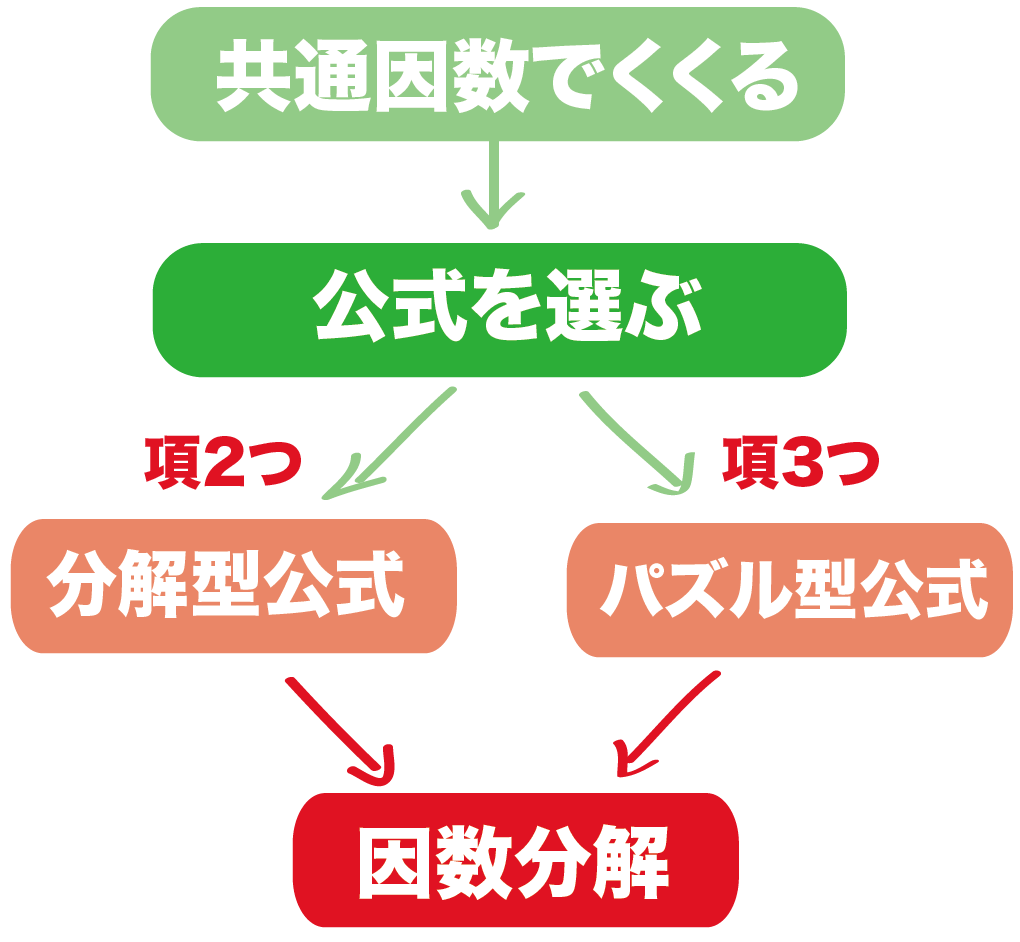
今回は因数分解の応用問題でもややこしいものを扱いました。 ここまでできれば大抵の場合は大丈夫ではないでしょうか? 中学生でこれ以上の問題が必要になることはまれだと思います。 因数分解はある程度たくさんの問題を解いた方が上達が早いです。中学校数学では文字を含む多項式の因数分解が非常に重要になります。 多項式の因数分解の手順 中学校数学の範囲では多項式の因数分解は以下の手順で行います。 最大の共通因数(すべての項に共通の因数)でくくる;まずは、\(x^2y^22xy\)と\(2x2y\)をそれぞれ因数分解します。 その後、\(xy=A\)と置き換えを利用して因数分解をしていきましょう。 $$x^2y^22xy2x2y$$ $$=(xy)^22(xy)$$ $$=A^22A$$ $$=A()$$ $$=(xy)(xy2)$$
因数分解 中学 応用のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  | |
「因数分解 中学 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 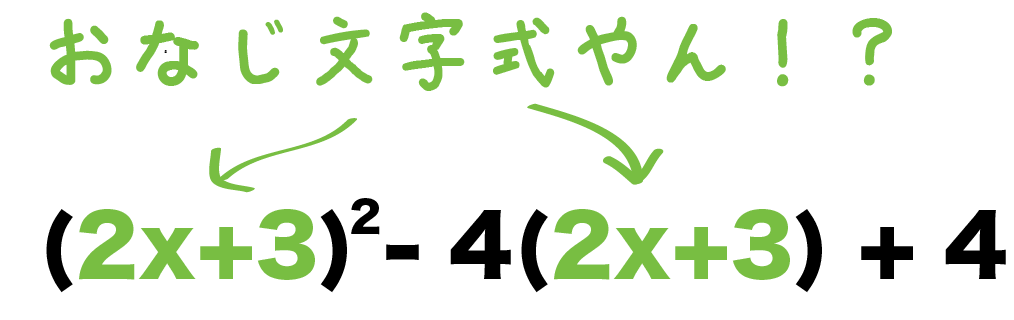 | 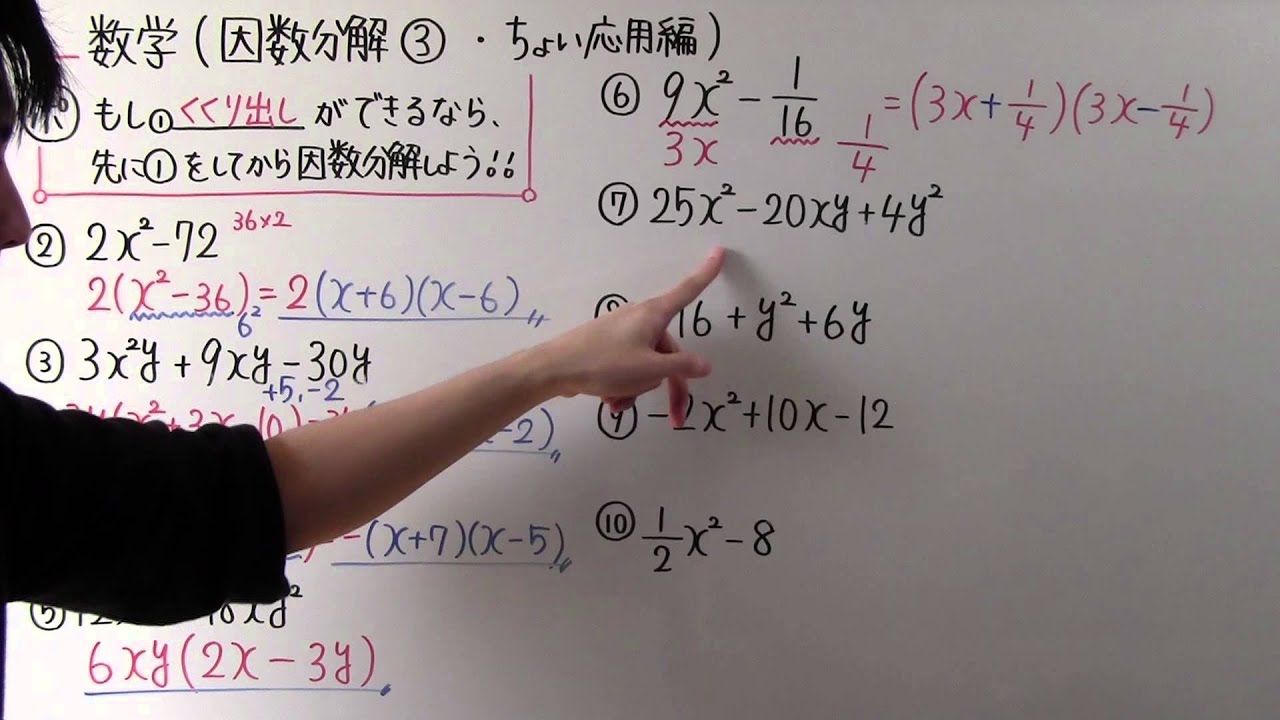 |
 |  |  |
「因数分解 中学 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「因数分解 中学 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「因数分解 中学 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「因数分解 中学 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「因数分解 中学 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「因数分解 中学 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 | ||
「因数分解 中学 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「因数分解 中学 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「因数分解 中学 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「因数分解 中学 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
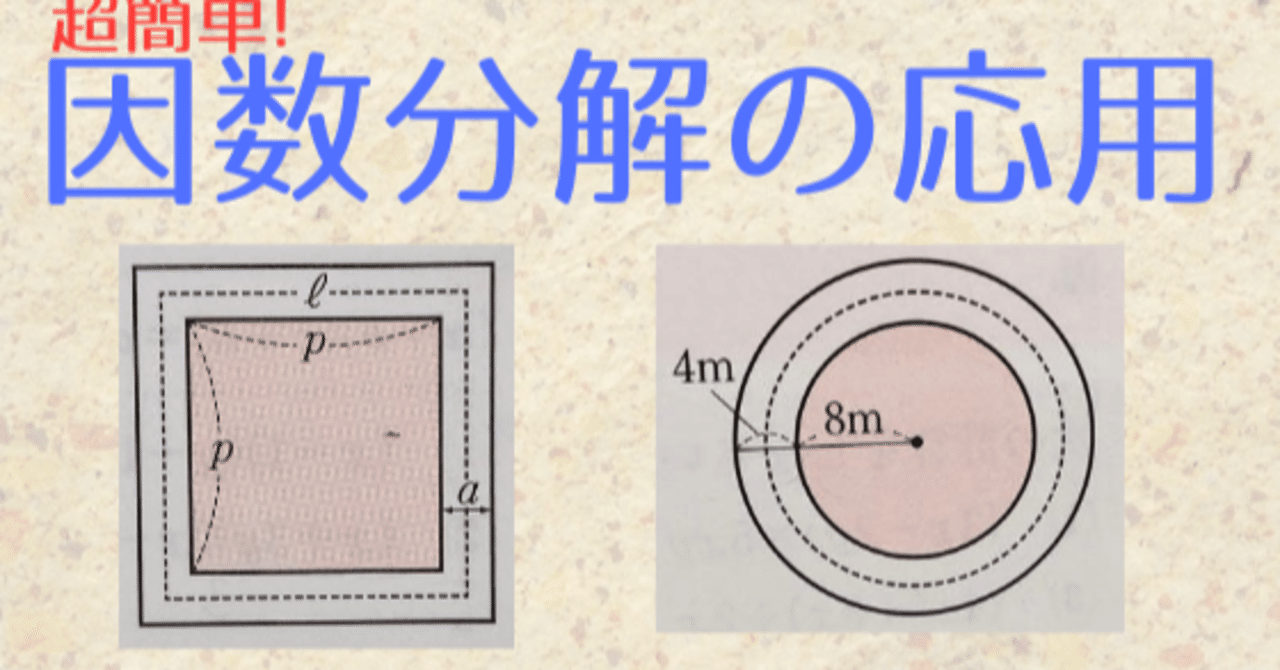
今回は因数分解の応用問題のやり方を解説します。 応用問題とは、こんなの↓ 例21)\( 3x^2 75 \) 例31)\( (x1)^2 4(x1) 3 \) 例41)\( 2a(b5) 3b15 \) つまり、 共通因数でくくってさらに公式を使う問題;因数分解共通因数でくくるやり方まとめ! お疲れ様でした! 以上、共通因数でくくり因数分解のやり方でした。 共通因数でくくるというのは、ちょっと慣れが必要かもしれませんが何度も練習していれば苦労なく解くことができるようになります。
コメント
コメントを投稿