【ベストコレクション】 ��形 の 求め 方 265496

扇形の弧の長さの公式と求め方 扇形の弧の長さの公式は下記です。 l=rθ ※lは弧の長さ、rは扇形の半径、θは角度（ラジアン） 半径5、角度が36°の扇形があります。扇形の弧の長さを求めてください。 ポイントは角度36°をラジアンに変換することです。 「扇形の弧の長さ」の求め方の基本はわかったね？ ？ それじゃあ、 扇形の弧の長さの公式 をみていこう！ 扇形の半径をr、中心角をα、円周率をπとすると、 2πr×α/360 で「扇形の弧の長さ」を求められるんだ。 公式のうしろにある「 α/ 360 」という数値が「 扇形が円の 分の1になっている 」ってことをあらわしているよ。 つまり、「円」という1枚のピザを何等分に切ったか？ ？ とい 完全な円の面積（ πr2 π r 2 ）と比べて、扇形の割合をかけた値が扇形の面積になります。 『半径×半径×314× 中心角 360 × 314 × 中 心 角 360 』⇒『πr2 × a 360 π r 2 × a 360 』 5扇形の面積の公式（弧の長さからの導出） 扇形について、以下のような問題が出題されることがあります。 半径 6cm 6 c m 、弧の長さ 10πcm 10 π c m の扇形の面積を求めよ。 今までの公式を利用したら

扇形の弧の長さの求め方 たぬぬ塾 中学校の先生たち

扇形 の 求め 方

扇形 の 求め 方- 扇形の周の長さの求め方 扇形の周の長さとは、扇形を1周した長さのことをいうので、次のように求めることができます。 つまり！ 弧の長さを求めて、半径を2個分出せばOKということです。 ゆい なんだ！ 単純だね♪ では、弧の長さの求め方を確認した上で問題を解いてみましょう扇形の面積の求め方 扇形の面積は、扇形の中心角を θ とした場合、 円の面積 × θ/360° で求めることができます。 つまり、半径が r の扇形であれば、面積は、 r^2π× θ/360° で求まります。 なお、 θ=360° のとき、円の面積になります。 中心角が弧度法の場合 中心角が弧度法の場合は

扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典

 扇形の部分が円の「何分の1」なのかがわかれば簡単に解くことができます。 つまり、円は360度なので、扇形の中心の角度がわかれば以下のような公式に当てはめるだけで問題を解くことができます。 おうぎ形の弧の長さ ＝ 直径 × 円周率 × 中心角 ÷ 360 扇形の面積 ＝ 半径 × 半径 × 円周率 × θ / 360 ・・・ ① 次に弧の長さを求めると以下のようになります。 弧の長さ ＝ 円周 × θ / 360 ＝ 2 × 半径 × 円周率 × θ / 360 この式を変形すると、 弧の長さ ÷ 2 ＝ 半径 × 円周率 × θ / 360 ・・・ ② となります。 ①と②の赤字部分を見てください。 同じですよね。 ここで②の左辺を①に代入すると、以下の式が出現します。 扇形の面積 ＝ 半径 × 弧の扇形の面積が三角形と等しいといったら信じられるだろうか？ 三角形の底辺と高さが、扇形のどこの部分の長さと等しいかを考えて、面積の公式を作ってみよう。 ＜ソフトウェアの使い方 に

面積がπ㎝²、中心角が40°であるおうぎ形の半径を求めなさい。 今度は面積が与えられているので おうぎ形の面積の公式に当てはめていきましょう。 すると、このような方程式ができあがります。 これを解いていきましょう！ 両辺をπで割って消し 面積や弧の長さを求める問題にも対応できるようになるよ じゃあ、具体的に見ていこうね 具体的に解く 中心角の求め方の問題は3パターン考えられるよ 弧の長さと半径が分かっている場合;ご意見・ご感想 いつも助かっています。 計算結果は問題ないのですが、参考の円弧の長さLの計算式 L=rθですが エクセルで半径×中心角とすると、計算の答えとエクセルの答えが違います。 どちらが正しいかわからないのでググったらL=314×半径×中心角/180という式の答えが 計算結果と同じになり

扇形の面積の公式と求め方 扇形の面積の公式は下記です。 S=r 2 θ/2 ※Sは扇形の面積、rは扇形の半径、θは扇形の角度（単位はラジアン） 公式を用いて、例題の扇形の面積を求めましょう。角度60°の扇形があります。半径が6です。面積を求めてください。円の直径と面積の公式では円周率を π とする 扇形の弧の長さと面積を出すためには、その前に円周と面積を必ず出さなければいけません。 そのため、小学校の算数のおさらいをしましょう。 円周や面積については、以下の公式によって計算します。 円周 ＝ 直径 × 314（円周率） 円の面積 ＝ 半径 × 半径 × 314（円周率） ただ中学数学では、円周率として314を 助詞の「わ」を「は」と書くと教育がないと思われます。 「こう」の長さは「弧」の長さでしょうか。 レポート課題ではなさそうなので、考え方だけ書きます。 扇形は中心角θで決ります。円について2πで決る量は比例計算で出ます。

おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ

2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく

扇形の面積と弧の長さの求め方 扇形の面積 S × a ∘ 360 ∘ 例1） 中心角が 90 ∘ で、弧の長さが 628 c m の扇形の一辺の長さを求めなさい。 分からない部分を x として計算式にあてはめて計算します。 扇形の一辺の長さ x は直径の半分の長さですから 扇形の面積 ＝ 底面の円の面積 ＋ 扇形の面積 ＝ R × R × π ＋ ( L × L × π ) × 2Rπ / 2Lπ ＝ R2 π ＋ LRπ これで、扇形の表面積を計算することができました。 毎回このように計算してももちろんよいのですが、この計算結果から1つの公式を求めることができます。 それは、 円錐の側面積 ＝ LRπ であるということです。 このような公式が隠れていました。 次回からはあっという間に計算比較 弧の長さ は、 r θ と表されるので、中心角に比例します。 一方、 弦の長さ は、 2 r sin θ 2 と表されるので、中心角には比例しません。 また、中心角が等しい場合、 弧の長さ は 弦の長さ よりも長いです。 どちらも、 0 ∘ ≤ θ ≤ 180 ∘ の範囲で

中心角40度 弧の長さ２pｃｍの扇形の面積中心角３０度 弧の長さpｃｍの扇形 Yahoo 知恵袋

中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット

 1 つ目の式を 2 つ目に代入するだけです。 1 つ目の式から θ = l r とできますので、弧度法の角度 θ を消せば S = 1 2 r 2 θ = 1 2 r 2 × l r = 1 2 r l となります。 もし 半径と弧の長さがわかっているのであれば 、その情報だけで 扇形の面積が出せる公式 です円周の長さ 2πr に対して、中心角の割合が θ/2π であるため もしくは、単純に、1ラジアンの円弧の長さ（＝半径（r））の θ倍であるため ・扇形の面積は （r 2 θ）/2 扇形の面積の公式：円弧×半径/2 に代入 もしくは、円全体の面積 πr 2 に割合 θ/2π を扇形の面積 r： θ： ラジアン： 面積： 円 円 半円 扇形 円周長から面積

中1 数学 中1 75 おうぎ形の弧と面積 基本編 Youtube

扇形の半径の求め方 計算のやり方をイチから解説していくぞ 中学数学 理科の学習まとめサイト

扇形 面積計算 公式 半径 角度 求め方 自動 円周率 ラジアンも計算 扇形 面積計算 公式 面積; 弧の長さ まずは、求めたい半径の大きさを ㎝とします。 すると、半径 ㎝で中心角1°の扇形の弧の長さは と表すことができます。 そして、弧の長さが ㎝になるはずだから という方程式が完成します。 あとは、これを解いていけば の値（半径）を求めることができます。 では、この方程式の解き方を順にみていきましょう。 まずは、両辺から を消し 扇形の半径を求める公式を教えてください！ 半径は半径=(弧の長さ)÷(円周率)÷(中心角)×180です。弧の長さの式から導き出せますね。 累積度数と累積相対度数の求め方をおしえてく

扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 Hatsudy 数学 科学

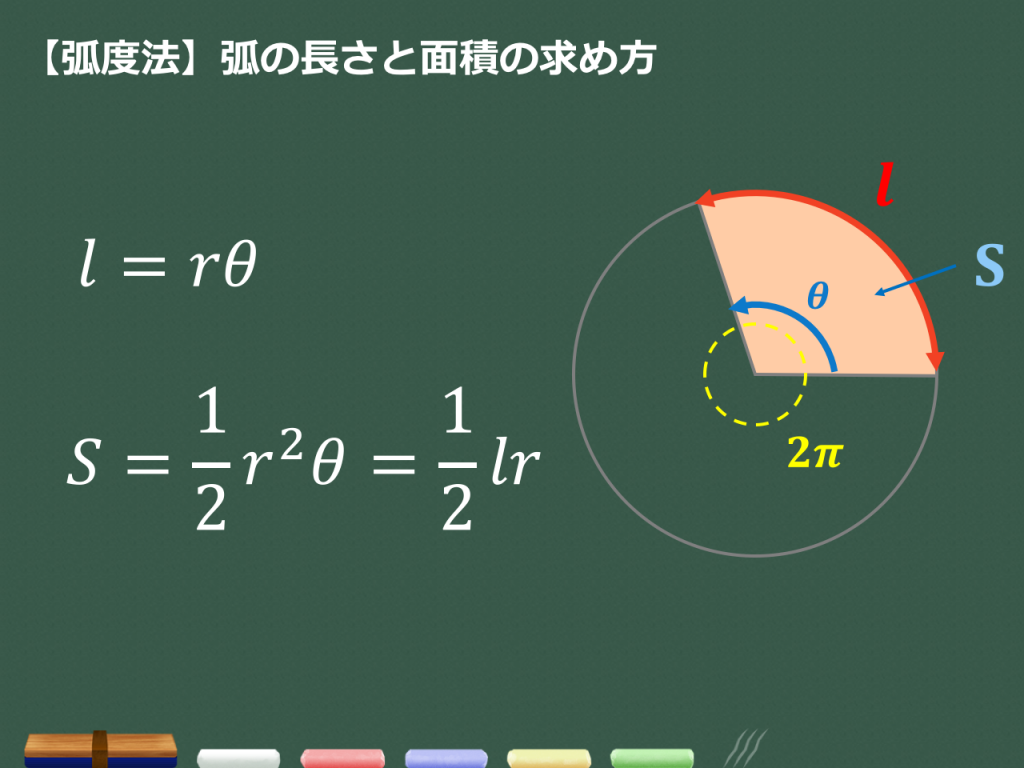
3分でわかる 弧度法 ラジアン の基礎知識 度数法との変換の仕方をわかりやすく 合格サプリ

扇形の面積 半径と中心角から扇形の面積・円弧の長さ・弦の長さを公式を使って計算します。 半径rと中心角θの値を入力し「扇形の面積を計算」ボタンをクリックすると、扇形の面積・円弧の長さ・弦の長さを計算して表示します。 半径 r：1 直径8の円の上半分の面積 直径が8だから半径は4．半円だから円の面積の半分：4 2π ÷2=8 π π 採点する やり直す 解説 2 半径 6 ，中心角が1°の扇形の面積 1°だから円（360°）の3分扇（おうぎ）形の面積を求める公式3つと弧の長さの求め方をお伝えします。 面積と弧の長さは比例ですべて解けるのですがこれを苦手にしている中学生はものすごく多いです。 これには当然とも言える理由が3つあります。 ここで図形を

扇の弧の長さと面積の求め方 公式 中学数学 By Okボーイ マナペディア

扇形の弧の長さの求め方 たぬぬ塾 中学校の先生たち

2 θ) r ( θ) 2 = a 2 b 2 b 2 cos 2 ⁡ θ a 2 sin 2 ⁡ θ ( 2) e l l i p t i c a l a r c h L = a E ( x ( θ 0) a, k) − a E ( x ( θ 1) a, k) x ( θ) = r ( θ) cos ⁡ θ, k = 1 − ( b a) 2, a ≥ b, π 2 ≥ θ ≥ 0 E ( x, k) 2 n d i n c o m p l e t e e l l i p t i c i n t e g r a l 扇形の半径R角度Θとします。 半径rの弧の重心x=ξとするとx=rcosθ ξ (rΘ)≡∫x (rdθ) =∫ (r^2)cosθdθ =2 (r^2)sin (Θ/2) 扇形の重心x=ηとすると η π (R^2) {Θ/ (2π)}=∫ξ (rΘdr) = (2/3) (R^3)sin (Θ/2) η= (4/3) {Rsin (Θ/2)}/Θ 1人 がナイス！ しています 質問者からのお礼コメント 助かりました！ お礼日時： 18/9/23 1134この扇形の中心角の大きさを求めよ。 円周は12×314cm。 これに 中心角 360° 中 心 角 360 ° をかけたら弧の長さ314cmになるということです。 円周と弧の長さの比は中心角が基準となっているということを抑えておきましょう。 中心角 360° 中 心 角 360 ° ＝ 314 12× 314 314 12 × 314 ＝ 5 6 5 6 5 6 5 6 のおうぎ形なので、中心角は 5 6 5 6 ×360°＝300°です。 おうぎ形の問題といえばこれらが

3

扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典

中心角 2本の半径がなす 角 を扇形の 中心角 という。 中心角が 180° のものは半円であり、円は中心角 360° の扇形と考えることもできる。 円Oから、2本の半径OA,OBが切り取る扇形を扇形O⌒ABと呼ぶ（⌒はABの上にかぶせて書くのが正しい）。 円を異なる2それぞれの図形の見方、考え方について学んでいきましょう！ おうぎ形の公式って何だっけ？ という方は、まずこちらの記事で復習しておいてね！ ⇒ おうぎ形面積、弧の長さ、中心角の求め方を問兵庫県の小学生 徳川 家康 さんからの解答。 いわゆる、《スーパー三角形》というものです。 参考 この問題は《スーパー三角形》ですが、この他に《スーパー台形》というものもあります。 円錐台の表面積を求めるのに役立ちます。

カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

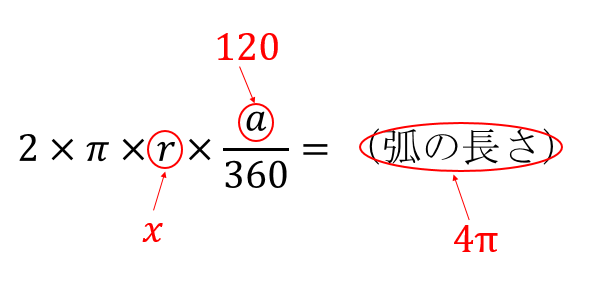
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ

 今回は、勉強のことだよ。 中心角が分からない扇形の面積の求め方の裏ワザだよ。 ↓これ この扇形の弧の長さを15㎝、 AからCの長さは10cmにするよ。 この問題を普通にやると、 15円弧の長さ (L) =B1*RADIANS (B2) 3 弦の長さ (c) =2*B1*SIN ( RADIANS (B2/2)) 2 面積 (S) =B1^2*RADIANS (B2)/2平面図形の面積・周長・重心位置の求め方 平面図形の面積（A） 周長（L） 重心位置（G） 型名 図形 公式 円 扇 形 弓 形 楕 円 方

扇形の中心角とは 求め方って 円周や面積や弧の長さを使って計算 ノビコト

高校数学 一般角と弧度法 扇形の弧長l R8と面積s 1 2r 8 受験の月

扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ

扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典

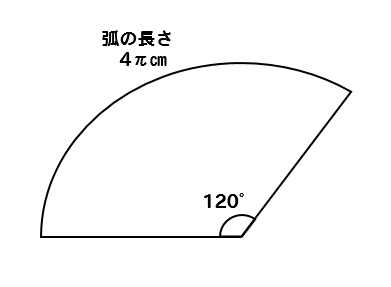
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ

写真の底面が扇形の立体の表面積の求め方を教えてください 特に側面積が Yahoo 知恵袋

しぶん い は ん い 求め 方 説明表現 んです のです ２ Stg Origin Aegpresents Com

扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典

3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ

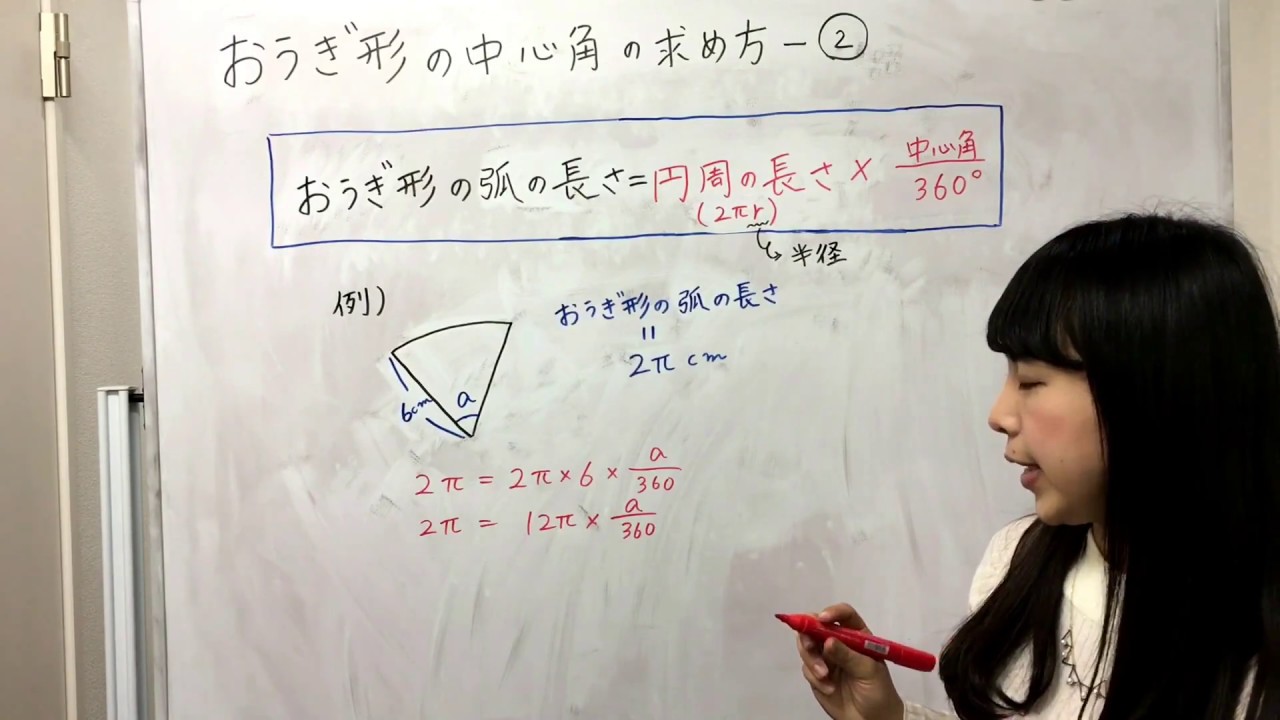
中1数学 おうぎ形の中心角の求め方 家庭教師のガンバ Youtube

扇形の弧の長さと面積 計算ドリル 問題集 数学fun

数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

円錐の表面積の求め方 You Look Too Cool

扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ

おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun

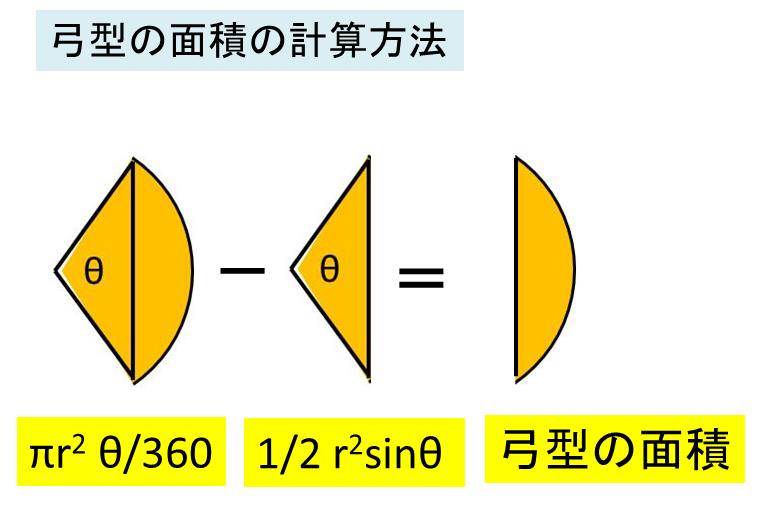
欠けた円 欠円 や弓形の面積の計算方法

中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく

カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ

中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく

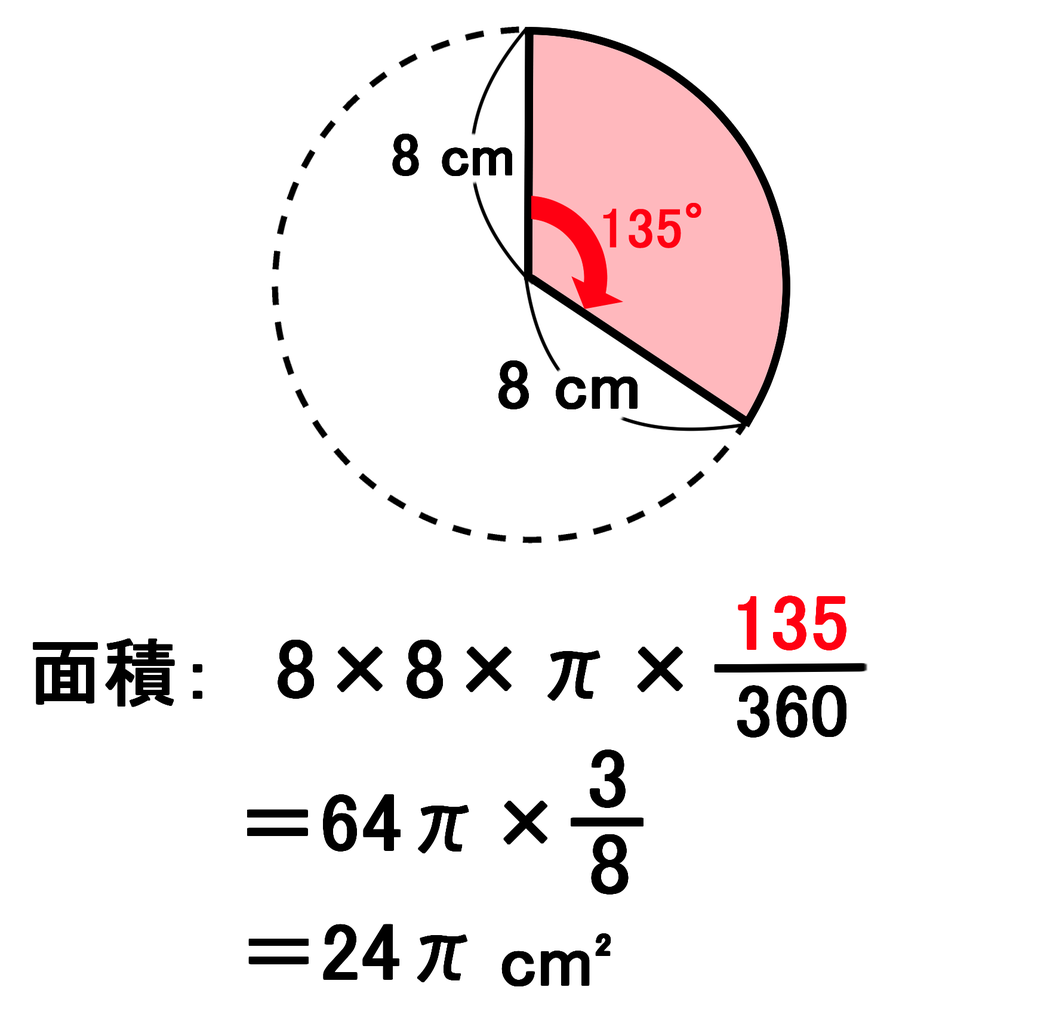
おうぎ形の面積と弧の長さの求め方 バカでもわかる 中学数学

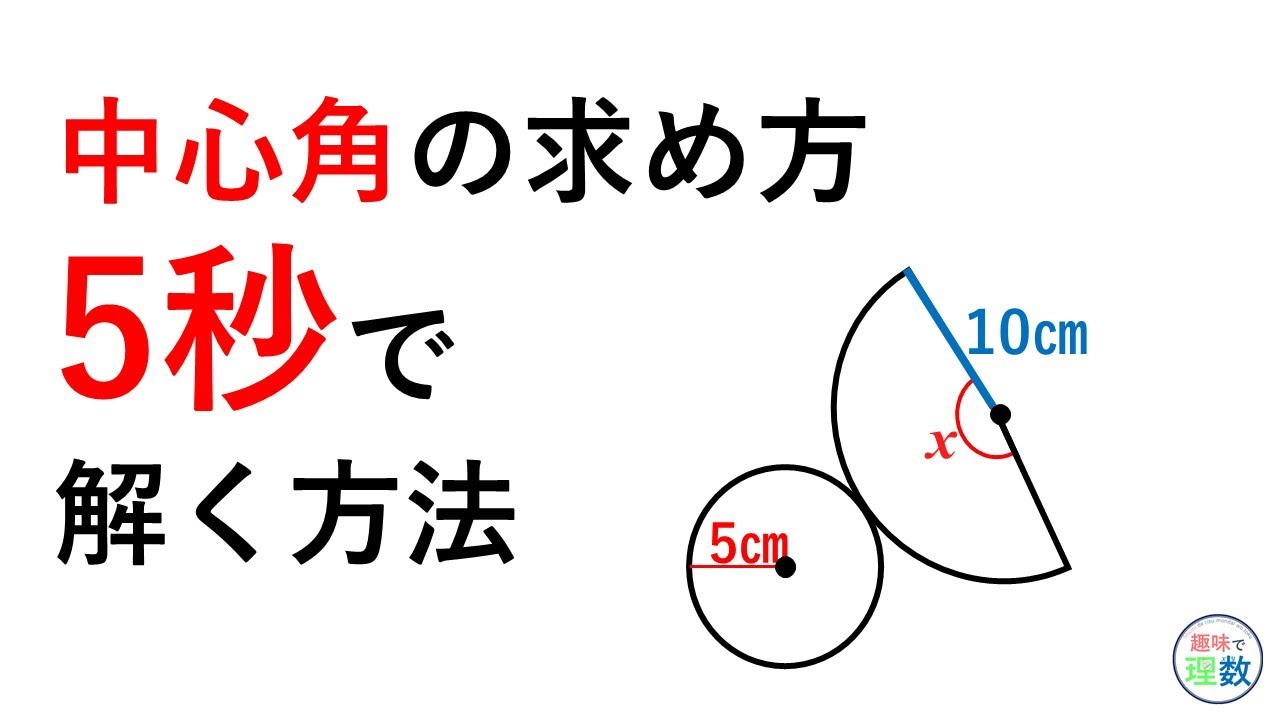
おうぎ形の中心角の求め方 Youtube

三角形と扇形の面積 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc

円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト

扇形の面積 Geogebra

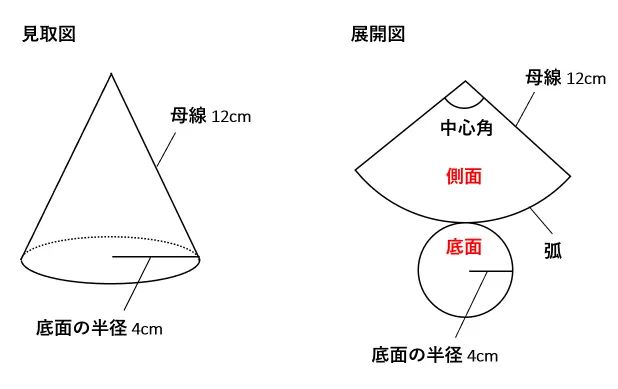
円錐の表面積を公式で求めよう 母線と底面の半径だけで簡単に計算できる 中学受験ナビ

扇形の面積の求め方 公式と計算例

扇形 中心角 公式 学び 教科書 勉強

扇形の中心角の求め方

半径4cm面積6pcm の扇形の中心角の求め方を教えてください Yahoo 知恵袋

2

扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題

物理のための数学 図のbを含む扇形の面積の求め方を教えてくださいますでしょう Yahoo 知恵袋

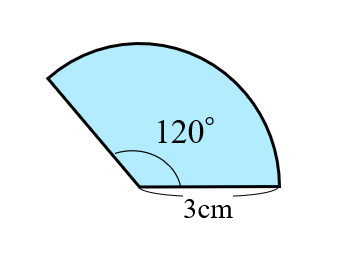
円 扇形 の面積 周や弧の長さの公式 数学fun

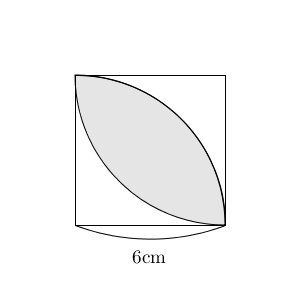
標準 おうぎ形と正方形の面積 なかけんの数学ノート

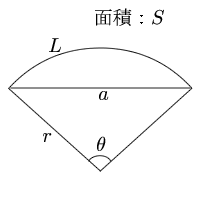
扇形 面積の計算 計算サイト

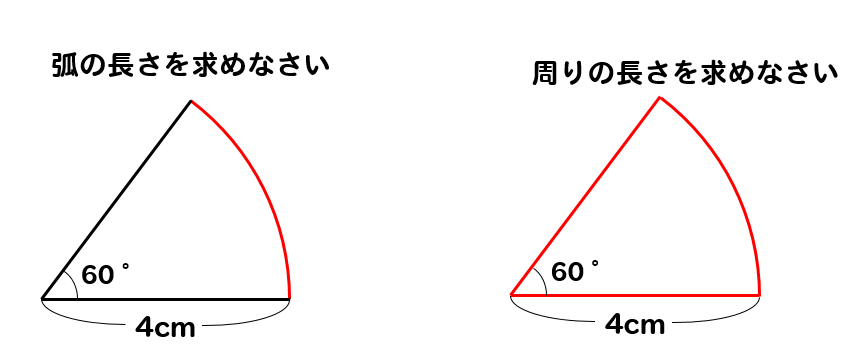
おうぎ形 注意 周りの長さを求める公式を解説 数スタ

円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学

扇形の面積の出し方と特殊な場合の公式 たぬぬ塾 中学校の先生たち

3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ

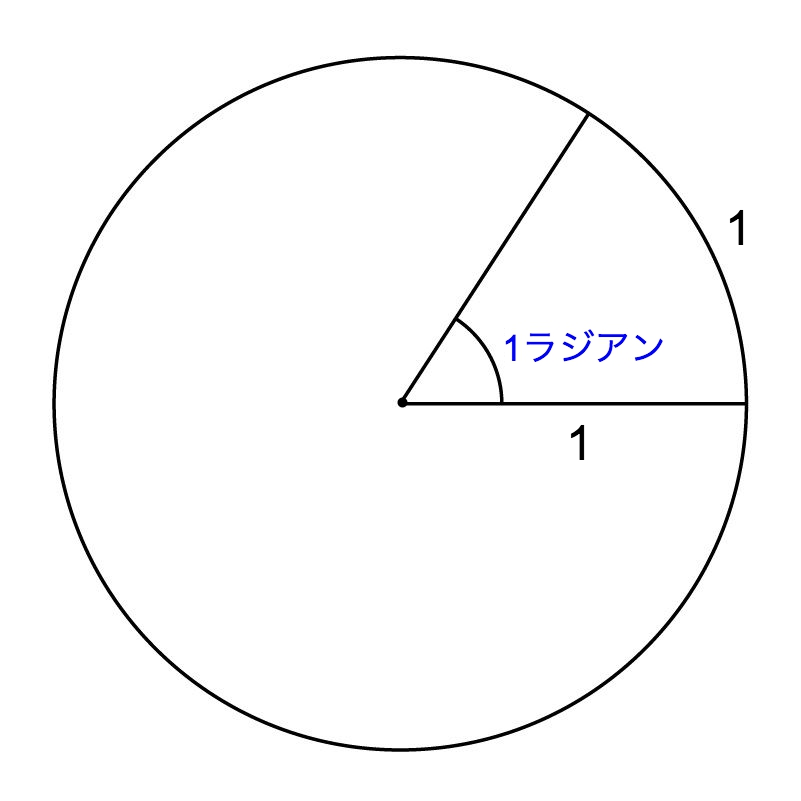
扇形の弧の長さと面積の求め方 Joyplotドキュメント

扇形 周の長さの求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト

扇形と扇形が重なっている部分の面積の解き方を教えてください 円周率 中学校受験 教えて Goo

円 扇形 の面積 周や弧の長さの公式 数学fun

Download Qikeru Images For Free

扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典

扇形の弧の長さの求め方 公式と計算例

中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット

数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

扇形 周の長さの求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト

半径9cm 面積18pcm の扇形の中心角を求めなさいという問 Yahoo 知恵袋

円錐の側面積 展開図の扇形の中心角 扇形の面積の求め方について 身勝手な主張

2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく

扇 おうぎ 形の面積を求める公式と弧の長さの求め方

扇形 周の長さの求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト

3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ

扇形の重心 物理実験集 管理人の近況報告ブログ

扇形 中心角 公式 学び 教科書 勉強

扇形の面積を半径 中心角 弧の長さから求める2通りの方法 偏差値40プログラマー

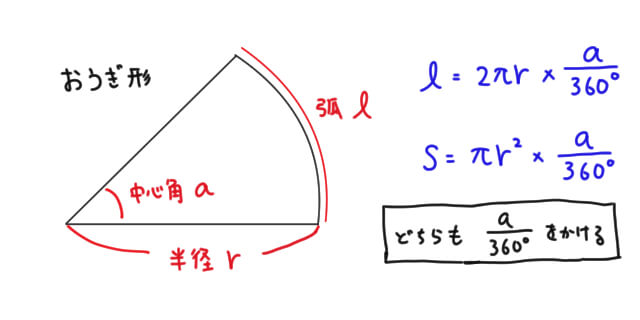
おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook

円 扇形 の面積 周や弧の長さの公式 数学fun

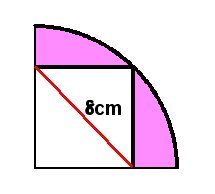
扇形と正方形

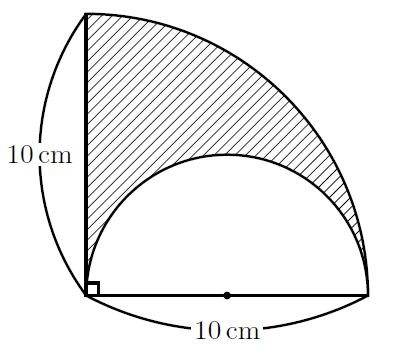
中学数学 扇形の面積 長さの瞬殺技 頻出図形 数樂管理人のブログ

扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ

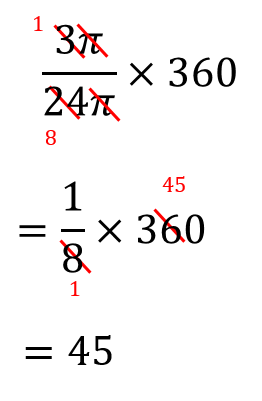
おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ

扇形の面積の求め方 公式と計算例

扇形の面積 弧の長さ まわりの長さの求め方 公式 小学生 中学生の勉強

扇形の中心角の求め方 面積と半径がわかっているパターン Youtube

扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 Hatsudy 数学 科学

扇形の中心角の求め方を教えてください 中心角の求め方は２通りのパタ Yahoo 知恵袋

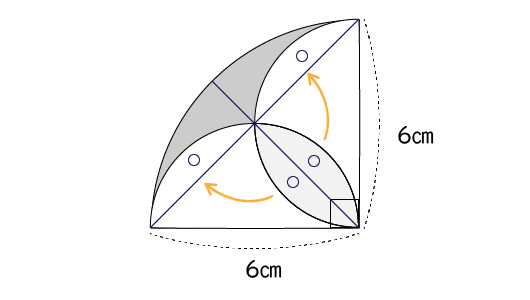
中学校1年生数学 複雑な面積の求め方 成果主義 Itto個別指導学院 長野市の学習塾

円弧面積の計算式

オンラインショップ セーフラン ドア路面標識ステッカー 半径10mm4分の1円扇形 黄 通販 2ebefd94 正規販売店 Aseraseo Com

おうぎ形の問題 ちょっと応用編 切り取って求める 苦手な数学を簡単に

円 扇形 の面積 周や弧の長さの公式 数学fun

扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ

3

扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題

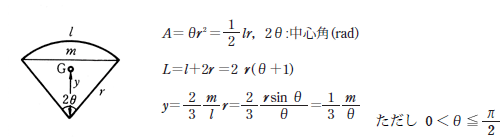
平面図形の面積 A 周長 L および重心位置 G 扇形 P11

Wb 扇形の回転体の体積の求め方

扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典